Question

What is the boiling point of a solution containing 0.144 g of eugenol dissolved in 10.0 g of benzene

Answer 1

Answer: The boiling point of solution is 80.32°C

Step-by-step explanation:

To calculate the molality of solution, we use the equation:

`\text{Molality of the solution}=\frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ in grams}}`

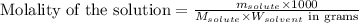
Where,

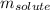`m_(solute)` = Given mass of solute (eugenol) = 0.144 g

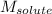`M_(solute)` = Molar mass of solute (eugenol) = 164.2 g/mol

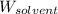`W_(solvent)` = Mass of solvent (benzene) = 10.0 g

Putting values in above equation, we get:

`\text{Molality of eugenol}=(0.144* 1000)/(164.2* 10.0)\\\\\text{Molality of eugenol}=0.088m`

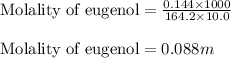
To calculate the elevation in boiling point, we use the equation:

`\Delta T_b=iK_bm`

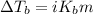
where,

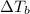`\Delta T_b` = elevation in boiling point =
`\text{Boiling point of solution}-\text{Boiling point of pure solution}`

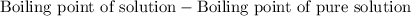
Boiling point of pure solution (benzene) = 80.1°C

i = Vant hoff factor = 1 (For non-electrolytes)

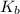`K_b` = molal boiling point elevation constant = 2.53°C/m

m = molality of solute = 0.088 m

Putting values in above equation, we get:

`\text{Boiling point of solution}-80.1=1* 2.53^oC/m* 0.088m\\\\\text{Boiling point of solution}=0.22+80.1=80.32^oC`

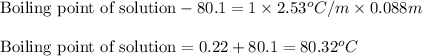
Hence, the boiling point of solution is 80.32°C