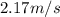Question

A 332 kg mako shark is moving in the positive direction at a constant velocity of 2.30 m/s along the bottom of a sea when it encounters a lost 19.5 kg scuba tank. Thinking the tank is a meal, it has lunch. Assuming momentum is conserved in the collision, what is the velocity of the shark immediately after it swallows the tank?

Answer 1

To solve this problem we will apply the concepts related to the conservation of momentum. By definition we know that the initial moment must be equivalent to the final moment of the two objects therefore

`p_1 = p_2`

`m_1u_1+m_2u_2 = m_1v_1+ m_2v_2`

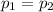
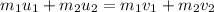
Here,

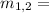`m_(1,2) =` Mass of each object

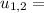`u_(1,2) =` Initial velocity of each object

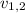`v_(1,2)`= Final velocity of each object

Since the initial velocity relative to the metal tank is at rest, that velocity will be zero. And considering that in the end, the speed of the two bodies is the same, the equation would become

`m_1u_1 = (m_1+m_2)v_f`

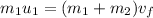
Rearranging to find the velocity,

`v_f = (m_1u_1)/( (m_1+m_2))`

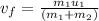
Replacing we have that,

`v_f = ((332)(2.3))/( (332+19.5))`

`v_f = 2.17 m/s`

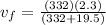
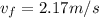
Therefore the velocity of the shark immediately after it swallows the tank is
`2.17m/s`