Answer:
The probability of picking a red marble and a blue marble = 6/25
Explanation:
Here, the question is INCOMPLETE.
What is the probability of this independent event. Drawing a red marble from a bag of 6 red and 4 blue marbles, replacing it, and then drawing a blue marble.
Here, total number of red marble in bag = 6
total number of blue marble in bag = 4
So, total marbles in the bag = 6 + 4 = 10 marbles
Now,if E : Any given event, then
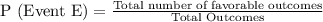
So, here
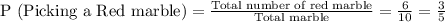
⇒ P(a Red ball) = 3/5 ...... (1)
Now, if the picked marble is REPLACED, then total marbles in the bag = 10
So, here

⇒ P(a Blue marble) = 2/5 ...... (2)
So, the probability of picking a red marble and a blue marble AFTER REPLACING
=P(a Red marble) x P(a Blue marble) = 3/5 x 2/5 = 6 /25
Hence, the probability of picking a red marble and a blue marble = 6/25