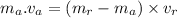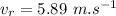Question

A model air rocket with a mass of 50.g is free to travel along a horizontal track. It begins from rest. After 2.0s, the rocket has lost 10% of its mass by expelling air at an average velocity of 53.m⋅s−1. What is the velocity of the rocket at that moment

Answer 1

`v_r=5.89\ m.s^(-1)`

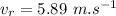
Step-by-step explanation:

Given:

• mass of rocket,
  `m_r=50\ g`

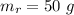
• time of observation,
  `t=2\ s`

• mass lost by the rocket by expulsion of air,
  `m_a=10\%\ of m_r=5\ g`

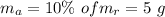
• velocity of air,
  `v_a=53\ m.s^(-1)`

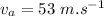
Now the momentum of air will be equal to the momentum of rocket in the opposite direction: (Using the theory of elastic collision)

`m_a.v_a=(m_r-m_a)* v_r`

`5* 53=(50-5)* v_r`

`v_r=5.89\ m.s^(-1)`