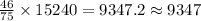Question

a week before election day, 276 out of 450 people said they would vote for the republican candidate. if 15,240 registered voters plan to vote, how many votes would you expect the republican candidate to get? [a] write a proportion that is defined by this situation. [b] explain how to cross product is used to solve the problem. [c] answer the question.

Answer 1

[A] The ratios can be written LaTeX: \frac{\text{republican votes}}{\text{total votes}}republican votes total votes. So we can write the proportion LaTeX: \frac{276}{450} = \frac{x}{15240}276 450 = x 15240.

[B] Use the cross product to get 450x = 4,206,240. Divide to get x = 9347.2.

[C] The republican can estimate that he will get 9347 votes.

Answer 2

(a)
`\frac {276}{450}=\frac {y}{15240}`

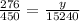
(b) We cross multiply the probability by the total voters

(c) 9347

Explanation:

(a)

Probability of getting a republican voter is

`\frac {276}{450}=\frac {138}{225}=\frac {46}{75}`

`\frac {276}{450}=\frac {138}{225}=\frac {46}{75}=\frac {y}{15240}`

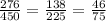
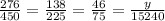
These are found by dividing the first numerator and denominator by 2, then by 3

To make it complete, the situation is therefore defined as
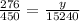`\frac {276}{450}=\frac {y}{15240}` where y is unknown value

(b)

Cross multiplication of the probability and number of voters gives the actual figure of y in the equation formed in part a of the question.

(c)

Since we have 15240 voters who plan to participate in election, we cross multiply to get the approximate number of republican voters which yields

`\frac {46}{75}* 15240=9347.2\approx 9347`