Question

A sinusoidal wave is travelling on a string under tension T = 8.0(N), having a mass per unit length of ï­1= 0.0128(kg/m). Itâs displacement function is D(x,t) = Acos(kx - ï·t). Itâs amplitude is 0.001m and its wavelength is 0.8m. It reaches the end of this string, and continues on to a string with ï­2 = 0.0512(kg/m) and the same tension as the first string. Give the values of A, k, and ï·, for the original wave, as well as k and ï· the reflected wave and the transmitted wave.

Answer 1

Step-by-step explanation:

For original wave,

Given:
`D(x,t) = Acos(kx - \omega t)`

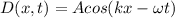
A=amplitude of incident wave=0.001m

V=speed of wave

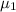`\mu_1`=linear mass density

T=tension in string

`K=(2\pi)/(\lambda_1)=(2\pi)/(0.8)=7.854m^(-1)`

`\omega=VK=K\sqrt{(T)/(\mu _(1))}=K\sqrt{(8.0)/(0.0128)}=196.35rad/s`

For reflected wave and transmitted wave ω remains same because frequency does not change. So

`\omega = 196.35rad/s`

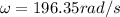
For reflected wave
`K=(2\pi)/(\lambda_1)=(2\pi)/(0.8)=7.854m^(-1)`

For transmitted wave
`K=(2\pi)/(\lambda_2)\\\\(V_1)/(V_2)=(\lambda_1)/(\lambda_2)=\sqrt{(\mu_2)/(\mu_1)}\\\\\lambda_2=0.8\sqrt{(0.0128)/(0.0572)}=0.4\\\\K=(2\pi)/(0.4)=15.708m^(-1)`