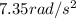Question

A rod of length L is hinged at one end. The moment of inertia as the rod rotates around that hinge is ML2 /3. Suppose a 2.00-m rod with a mass of 3.00 kg is hinged at one end and is held in a horizontal position. The rod is released as the free end is allowed to fall. What is the angular acceleration as it is released?

Answer 1

To solve this problem we will apply the concepts related to the moment of inertia and Torque, the latter both its translational and rotational expression.

According to the information given the moment of inertia of the body would be

`I = (1)/(3) mL^2`

Replacing we have

`I = (1)/(3) (3kg)(2m)^2`

`I = 4 kg * m^2`

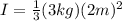
Now the translational torque would be the product between the force applied (Its own Weight) and the distance (Its center of mass at the middle)

`\tau = F*r`

`\tau = mg ((L)/(2))`

`\tau = (3)(9.8)((2)/(2))`

`\tau = 29.4N\cdot m`

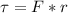
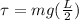
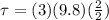
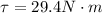
Now the rotational torque is defined as the product between the moment of inertia and the angular acceleration, then,

`\tau = I\alpha \rightarrow \alpha = (\tau)/(I)`

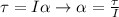
Replacing,

`\alpha = (29.4)/(4)`

`\alpha =7.35 rad / s^2`

Therefore the angular acceleration is
`7.35rad/s^2`