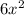The width of rectangle is
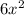
Solution:
Given that,
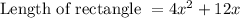
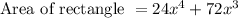
To find: width of rectangle
The area of rectangle is given by formula:

Therefore, width is given as:

Substituting the given values we get,
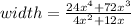
Factor out 24 and
 from numerator
from numerator
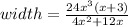
Factor out 4 and x from denominator
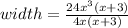
Cancel the common terms in numerator and denominator
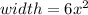
Thus the width of rectangle is