Question

Consider the probability distribution shown below.x 0 1 2P(x) 0.45 0.20 0.35Compute the expected value of the distribution.

Answer 1

The expected value of the distribution is 0.9

Explanation:

We are given the following probability distribution in the question:

x: 0 1 2

P(x): 0.45 0.20 0.35

We have to find the expected value of the given distribution.

The expected value of the distribution is the mean of the distribution.

Formula:

`E(x) = \displaystyle\sum x_iP(x_i)\\\\\text{Puttinf the values, we get,}\\E(x) = 0(0.45) + 1(0.20) + 2(0.35)\\E(x) = 0.9`

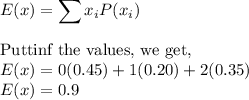
Thus, the expected value of the distribution is 0.9