Question

Find the area of quadrilateral ABCD whose vertices are A(1,1) B(7,-3) C(12,2) D(7,21)

Answer 1

The area of quadrilateral ABCD is 139 unit^2.

Explanation:

Given:

Quadrilateral ABCD whose vertices are A(1,1) B(7,-3) C(12,2) D(7,21).

Now, to find the area.

The coordinates of the quadrilateral are A(1,1), B(7,-3), C(12,2), D(7,21).

So, to find the area we need to bisect the quadrilateral ABCD and get the triangles ABC and ADC and then calculate their areas:

In Δ ABC:

`A(x_1,y_1)=(1,1)\:,\:B(x_2,y_2)=(7,-3)\:and\:C(x_3,y_3)=(12,2)`

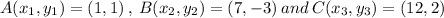
Now, to get the area of triangle ABC:

`Area\,of\,triangle\,=\,(1)/(2)\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|1(-3-2)+(7)(2-1)+12(1--3)\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|1(-5)+(7)(1)+12(4)\right|`

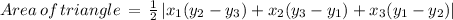
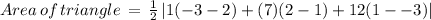
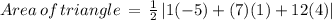
On solving we get:

`Area\,of\,triangle\,=25.`

In Δ ADC:

`A(x_1,y_1)=(1,1)\:,\:D(x_2,y_2)=(7,21)\:and\:C(x_3,y_3)=(12,2)`

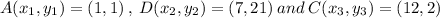
Now, to get the area of triangle ADC:

`Area\,of\,triangle\,=\,(1)/(2)\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|1(21-2)+(7)(2-1)+12(1-21)\right|`

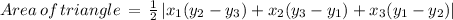
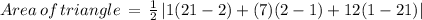
On solving it by same process as above we get:

`Area\,of\,triangle\,=114`

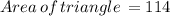
Now, to get the area of the quadrilateral we add the areas of the triangles ABC and ADC:

`25+114\\=25+114\\=139\ unit^2`

Therefore, area of quadrilateral ABCD is 139 unit^2.