Answer:
Option d is correct.
Explanation:
The point of inflection of a function y = f(x) at a pointy c is given by f''(c) = 0.
Now, the given function is
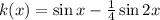
Differentiating with respect to x on both sides we get,
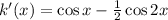
Again, differentiating with respect to x on both sides we get,
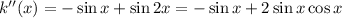
So, the condition for point of inflection at point c is
k''(c) = 0 = - sin c + 2 sin c cos c
⇒ sin c(2cos c - 1) = 0
⇒ sin c = 0 or
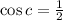
⇒ c = 0 or
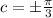
Therefore, option d is correct. (Answer)