Question

In a certain college, 33% of the math majors belong to ethnic minorities. If 7 students are selected at random from the math majors, what is the probability that: a. No more than 5 belong to an ethnic minority b. Exactly three of them belong to an ethnic minority c. None of them belong to an ethnic minority

Answer 1

Answer: a) 0.996, b) 0.253, c) 0.02.

Explanation:

Since we have given that

Probability of success = Probability of the math majors belong to ethnic minorities = 33% = 0.33 =p

Probability of failure = q = 1-0.33 = 0.67

Number of students selected = 7

a) No more than 5 belong to an ethnic minority

So, using "binomial distribution", we get that

`P(X\leq 5)=\sum^5 _(x=0) ^5C_x(0.33)^x(0.67)^(5-x)=0.996`

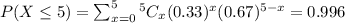
b. Exactly three of them belong to an ethnic minority

So, it becomes,

`P(X=3)=^7C_3(0.33)^3(0.67)^4=0.253`

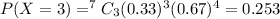
c. None of them belong to an ethnic minority

`P(X=0)=^7C_0(0.33)^0(0.67)^7=0.02`

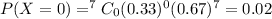
Hence, a) 0.996, b) 0.253, c) 0.02.