Answer:
vector equation:
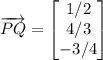
parametric equations:

Explanation:
The coordinates of the points are given as:
P(0,-1,1) and Q(1/2,1/3,1/4)
the coordinates of any points are also position vectors (vectors starting from the origin to that point), and can be represented as:
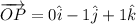
or

similarly,
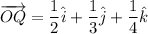
or
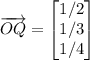
the vector PQ can be described as:
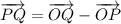

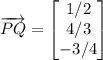
this is the vector equation of the line segment from P to Q.
to make the parametric equations:
we know that the general equation of a line is represented as:

here,
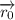 : is the initial position or the starting point. in our case it is the position vector of P
: is the initial position or the starting point. in our case it is the position vector of P
and
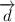 : is the direction vector or the direction of the line. in our case that's PQ vector.
: is the direction vector or the direction of the line. in our case that's PQ vector.
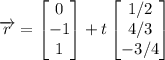
that parametric equations can now be easily formed:
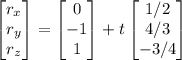

these are the parametric equations of the line PQ