Question

Stephanie has started a small company making organic honey she makes large and small containers. She has found the cost of running her business to have a linear relationship which can be 5.5x + 7.5y =930. She wants to sell a small container for $12 in a large container for $15 earn $1920. That creates a linear relationship modeled by 12x + 15y = 1920. how many of each kind of organic shpyld she sell fulfill her revenue and cost projections? (hint: 7.5* -2 = -15)​

Answer 1

Stephanie has sold 60 small containers and 80 large containers to fulfill her revenue and cost projections.

Explanation:

Given:

Equation modelling the cost of running her business =
`5.5x+7.5y=930 \ \ \ \ equation\ 1`

Also Given:

Cost of small container = $12

Cost of large container = $15

Total earnings is = $1920

Equation modelling his total earnings =
`12x+15y =1920 \ \ \ \ equation\ 2`

Now we need to find the number of each kind of containers she sold.

From above equation we can say that;

Number of small container is denoted by 'x'.

Number of large container is denoted by 'y'.

To find the number of each type of container she sold we will solve both the equations.

First we will will multiply equation 1 from 2 we get;

`2(5.5x+7.5y)=930*2\\\\11x+15y= 1860 \ \ \ \ equation \ 3`

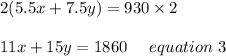
Now we will subtract equation 3 from equation 2 we get;

`12x+15y-(11x+15y)=1920-1860\\\\12x+15y-11x-15y = 60\\\\x= 60`

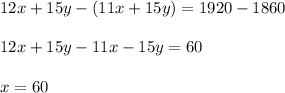
Now Substituting the value of 'x' in equation 1 we get;

`5.5x+7.5y = 930\\\\5.5* 60+7.5 y =930\\\\330+7.5y=930\\\\7.5y =930-330\\\\7.5y =600\\\\y=(600)/(7.5) = 80`

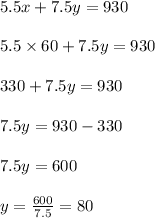
Hence Stephanie has sold 60 small containers and 80 large containers to fulfill her revenue and cost projections.