Question

Help me pls Represent the arithmetic series using the recursive formula.

94, 89, 84, 79, …

f(n) = f(1) + (−5)
f(n) = f(1) + (5)
f(n) = f(n − 1) + (−5)
f(n) = f(n − 1) + (5)

Answer 1

f(n) = f(n − 1) + (−5)

Explanation:

The answer is C. I took the test and earned a 100%

Answer 2

Option C) is correct

That is the given arithmetic sequence represents the recursive formula is f(n)=f(n-1)+(-5)

Explanation:

The given arithmetic sequence is
`{\{94,89,84,79,...}\}`

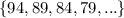
Let f(1)=94,f(2)=89,f(3)=84,...

To find the common difference d :

`d=f(2)-f(1)` ,

`=89-94`

`=-5`

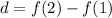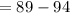
Therefore d=-5

`d=f(3)-f(2)` ,

`=84-89`

`=-5`

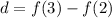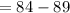
Therefore d=-5

Therefore the common difference d=-5

check the recursive formula
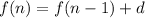`f(n)=f(n-1)+d` which represents the given arithmetic sequence

Put n=2 and d=-5 in
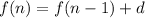`f(n)=f(n-1)+d` we get

`f(2)=f(2-1)+(-5)`

`=f(1)-5`

`=94-5`

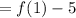
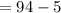
Therefore f(2)=89

Put n=3 and d=-5 in
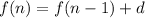`f(n)=f(n-1)+d` we get

`f(3)=f(3-1)+(-5)`

`=f(2)-5`

`=89-5`

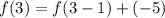
Therefore f(3)=84

and so on

Therefore the recursive formula
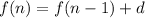`f(n)=f(n-1)+d` where d=-5

Therefore the recursive formula
`f(n)=f(n-1)+(-5)` represents the given arithmetic sequence