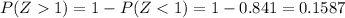Question

The incomes in a certain large population of college teachers have a normal distribution with mean $75,000 and standard deviation $10,000. Sixteen (16) teachers are selected at random from this population to serve on a committee. What is the probability that their average salary is more than $77,500?

0.0228

0.1587

0.8413

essentially 0

Answer 1

`P(\bar X >77500)=P(Z>(77500-75000)/(2500)=1)`

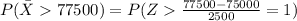
And using a calculator, excel ir the normal standard table we have that:

`P(Z>1)=1-P(Z<1) =1-0.841=0.1587`

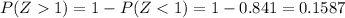
Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Solution for the problem

Let's say that X represent the random variable "incomes in a certain large population of college", and we know that the distribution for X is:

`X \sim N(\mu = 75000, \sigma= 10000)`

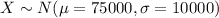
We select 16 teachers and we are interested on the sample mean or average, and we know that the distribution for the sample mean is given by:

`\bar X \sim N(\mu=7500,\sigma_(\bar X)= (\sigma)/(√(n))=(10000)/(√(16))=2500)`

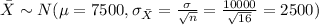
And we are interested on this probability:

`P(\bar X>77500)`

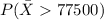
And we can use the z score given by:

`z = (\bar X -\mu)/(\sigma_(\bar X))`

`P(\bar X >77500)=P(Z>(77500-75000)/(2500)=1)`

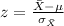
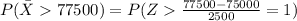
And using a calculator, excel ir the normal standard table we have that:

`P(Z>1)=1-P(Z<1) =1-0.841=0.1587`