Question

F(x) = b^x and g(x) = log b X are inverse functions. Explain why each of the following are true.

1. A translation of function f is f1(x) = b^(x-h). It is equivalent to a vertical stretch or vertical compression of function f.

2. The inverse of f1(x) = b^(x-h) is not equivalent to a translation of g.

3. The inverse of f1 (x) =b^(x-h) is not equivalent to a vertical stretch or vertical compression of g.

4. The function h(x) = log c X is a vertical stretch or compression of g or of its reflection -g. Read this as"negative g"

Will probably needs to use the properties of exponents and logarithms and change of base formulas to change the functions into alternate forms

Answer 1

1. A translation of function f is
`f_(1)(x)=b^(x-h)`. It is equivalent to a vertical stretch or vertical compression of function f.

Let's take the function:

`f_(1)(x)=b^(x-h)`

If we used the rules of powers, we know that when we have a subtraction in the power of an exponential, it can be split into a division. So the function can be rewritten as:

`f_(1)(x)=(b^(x))/(b^(h))`

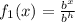
Remember the original function was:

`f(x)=b^(x)`

therefore:

`f_(1)(x)=(f(x))/(b^(h))`

this means that if
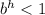`b^(h)<1` then it will be a vertical stretch.

If
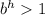`b^(h)>1` then it will be a vertical stretch.

2. The inverse of
`f_(1)(x)=b^(x-h)` is not equivalent to a translation of g.

This is partially true and you'll see why. Let's start by finding the inverse of that function:

`x=b^(y-h)`

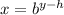
we start by turning the given power to a multiplication of powers so we get:

`x=b^(-h)b^(y)`

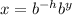
we then move the
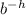`b^(-h)` to the other side of the equation so we get:

`xb^(h)=b^(y)`

and turn the equation into a logarithm:

`y=log_(b)(xb^(h))`

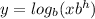
so:

`g_(1)(x)=log_(b)(xb^(h))`

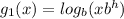
or:

`g_(1)(x)=g(b^(h)x)`

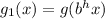
remember that when you multiply a constant by x, you will get a horizontal compression if
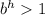`b^(h)>1` and a horizontal stretch if
`b^(h)<1`.

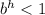but there is another interpretation for this function. Let's take the original equation:

`x=b^(y-h)`

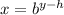
if we directly turned this equation into a logarithm we would get that:

`y-h=log_(b)(x)`

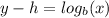
so:

`y=h+log_(b)(x)`

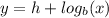
or:

`g_(1)(x)=h+g(x)`

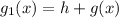
if the inverse function is written like this, it can be interpreted as a vertical shift. Both interpretations are correct.

3. The inverse of
`f_(1)(x)=b^(x-h)` is not equivalent to a vertical stretch or vertical compression of g.

As we saw in the previous part of the problem, that function is either a horizontal stretch/compression or a vertical shift, not a vertical stretch or compression.

4. The function
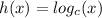`h(x)=log_(c)(x)` is a vertical stretch or compression of g or of its reflection -g.

We can rewrite the function like this thanks to log rules:

`h(x)=(log_(b)(x))/(log_(b)(c))`

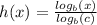
which is the same as:

`h(x)=(g(x))/(log_(b)(c))`

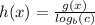
If
`log_(b)(c)>1` it will be a vertical compression of g(x). If
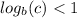`log_(b)(c)<1`, then it will be a vertical stretch no matter if g is positive or negative.