Question

Assume that P(A) = 0.4 and P(B) = 0.7. Making no further assumptions on A and B, show that P(AB) satisfies 0.1 ⤠P(AB) ⤠0.4.

Answer 1

Explanation:

Given that P(A) = 0.4 and P(B) = 0.7.

No further information is known about A or B

But we can say that from addition theorem of probability that

`P(AUB) = P(A)+P(B)-P(A B)\leq 1`

`i.e. P(AB) \geq 0.4+0.7-1 = 0.1\\`

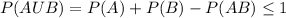
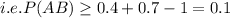
The greatest value P(AB) can take will be

since P(A) is less than P(B)

If one is a subset of Other, only A can be a subset of B.

If one set is a subset of other then we have maximum probability for their intersection.

Here P(AB) cannot exceed 0.4 the probability of smaller set A

Put together

P(AB) lies between 0.1 and 0.4