Question

spring-loaded toy gun projects a 5.9 g nerf pellet horizontally. The spring constant is 8.5 N/m, the barrel of the gun is 17 cm long, and a constant frictional force of 0.037 N exists between the barrel and the nerf pellet. If the spring is compressed 6.8 cm for this launch, determine the speed (in m/s) of the pellet as it leaves the barrel. (Assume the pellet is in contact with the barrel for the full length of the barrel.) m/s

Answer 1

`v=5.5836\ m.s^(-1)`

Step-by-step explanation:

Given:

• mass of pellet,
  `m=5.9* 10^(-3)\ kg`

• spring constant of the gun,
  `k=8.5\ N.m^(-1)`

• length of the barrel,
  `l=0.17\ m`

• frictional force offered by the barrel,
  `f=0.037\ N`

• compression of the spring,
  `\delta x=0.068\ m`

Spring force on the pellet:(inside the barrel)

`F=k.\delta x`

`F=8.5* 0.068`

`F=0.578\ N`

Net force on the pellet:(INSIDE THE BARREL)

`F_n=F-f`

`F_n=0.578-0.037`

`F_n=0.541\ N`

Acceleration of the pellet:(inside the barrel)

`a=(F_n)/(m)`

`a=(0.541)/(0.0059)`

`a=91.6949\ m.s^(-2)`

Using the equation of motion:

`v^2=u^2+2a.l`

where, v & u are the final and initial velocities respectively

`v^2=0^2+2* 91.6949* 0.17`

`v=5.5836\ m.s^(-1)` is the velocity at the exit of the barrel

Answer 2

Solution:

As per the question:

Mass of the pellet, m = 5.9 g = 0.059 kg

Spring constant, k = 8.5 N/m

Length of the barrel, l = 17 cm = 0.17 m

Frictional force, F = 0.037 N

Compression in spring,
`\Delta x = 6.8\ cm = 0.068\ m`

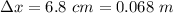
Now,

To calculate the speed of the pellet:

Using the principle of conservation of energy:

Change in spring potential energy is used in doing work against the friction force and provides the required kinetic energy:

`(1)/(2)k\Delta x^(2) = (1)/(2)mv^(2) + Fl`

`(1)/(2)* 8.5* 0.0068^(2) = (1)/(2)* 5.9* 10^(- 3)* v^(2) + 0.037* 0.17`

`v^(2) = 0.2797`

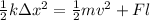
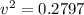
v = 0.5289 m/s