Question

An electron remains suspended between the surface of the Earth (assumed neutral) and a fixed positive point charge, at a distance of 8.88 m from the point charge. The acceleration of gravity is 9.8 m/s^2 and the value of Coulomb's constant is 8.98755 x 10^9 Nm^2/C^2. Determine the charge required for this to happen. Mass of electron is 9.10939 x 10^-31 kg.

Answer 1

To solve this problem we will apply the concept related to the balance of forces. Here the electrostatic force defined by Coulomb's laws must be proportional to the weight of the electron, defined by Newton's second law, so that such balance exists, both can be described as:

`F_e = (kq_1q_2)/(d^2)`

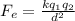
Here,

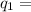`q_1 =` Charge required

`q_2 =`Charge of electron

d = Distance

k = Coulomb's constant

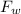`F_w` = mg

Here,

m = mass

g = Gravitational acceleration

In equilibrium the sum of Force is zero, then,

`\sum F = 0`

`F_e = F_w`

`(kq_1q_2)/(d^2) = mg`

`((8.98755*10^9 )(q_1)(1.6*10^(-19)))/(8.8^2) = (9.8)(9.10939*10^(-31) )`

`q_1 = 4.8075*10^(-19)C`

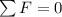
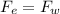
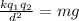
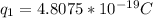
Therefore the charge required for this to happen is
`4.8075*10^(-19)C`