Answer:
(a) $200, 000, z-score= 3 and it is unusual.
(b) $55,000, z-score= -6.67 and it is unusual.
(c) $175,000, z-score= 1.33 and it is usual.
(d) $122,000, z-score= -2.2 and it is unusual
Step-by-step explanation:
Given: Mean of sample= $155000
Standard deviation= $15000.
Now, calculating z-score of each given prices.
z-score=
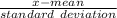
(a) Price= $200000
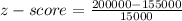
⇒
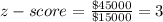
It is unusual as score is very high.
b) $ 55000
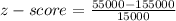
⇒
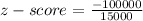
∴
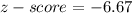
It is unusual again as score it very low.
c) $ 175000
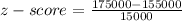
⇒
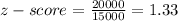
It is usual as score is in the top 0.30
d) $122000
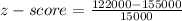
⇒
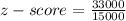
∴
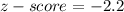
It is unusual as score is too low