Answer:
(a)
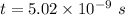
(b)

Step-by-step explanation:
It is given that,
Initial speed of an electron,
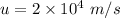
Final speed of an electron,
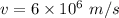
Distance, d = 1.5 cm = 0.015 m
(b) If a is the acceleration of the electron. It is given by the rate of change of its velocity. It can be calculated using third equation of motion as :
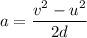
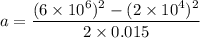

(a) Let t is the time interval in which the electron travel 1.50 cm. It is given by :
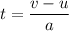
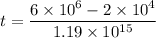
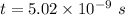
So, the time interval in which the electron travel 1.50 cm is
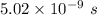 .
.
Hence, this is the required solution.