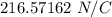Question

How many excess electrons must be distributed uniformly within the volume of an isolated plastic sphere 23.0 cm in diameter to produce an electric field of 1150N/C just outside the surface of the sphere? What is the electric field at a point 15.0 cm outside the surface of the sphere?

Answer 1

10573375000

`216.57162\ N/C`

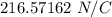
Step-by-step explanation:

k = Coulomb constant =
`8.99* 10^(9)\ Nm^2/C^2`

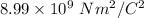
r = Distance =
`(d)/(2)=(23)/(2)=11.5\ cm`

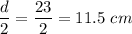
E = Electric field = 1150 N/C

Electric field is given by

`E=(kq)/(r^2)\\\Rightarrow q=(Er^2)/(k)\\\Rightarrow q=(1150* 0.115^2)/(8.99* 10^9)\\\Rightarrow q=1.69174* 10^(-9)\ C`

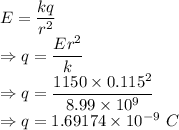
Number of electrons is given by

`n=(1.69174* 10^(-9))/(1.6* 10^(-19))\\\Rightarrow n=10573375000`

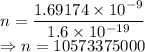
Number of excess electrons is 10573375000

r = 0.115+0.15 = 0.265 m

`E=(kq)/(r^2)\\\Rightarrow E=(8.99* 10^9* 1.69174* 10^(-9))/(0.265^2)\\\Rightarrow E=216.57162\ N/C`

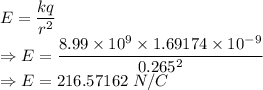
The electric field is
`216.57162\ N/C`