Question

A sample of CH4 is confined in a water manometer. The temperature of the system is 30.0 °C and the atmospheric pressure is 98.70 kPa. What is the pressure of the methane gas, if the height of the water in the manometer is 30.0 mm higher on the confined gas side of the manometer than on the open to the atmosphere side. (Density of Hg is 13.534 g/mL).

Answer 1

Step-by-step explanation:

The given data is as follows.

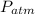`P_(atm)` = 98.70 kPa = 98700 Pa,

T =
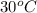`30^(o)C` = (30 + 273) K = 303 K

height (h) = 30 mm = 0.03 m (as 1 m = 100 mm)

Density = 13.534 g/mL =
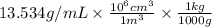
`13.534 g/mL * (10^(6)cm^(3))/(1 m^(3)) * (1 kg)/(1000 g)`

= 13534
`kg/m^(3)`

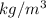
The relation between pressure and atmospheric pressure is as follows.

P =
`P_(atm) + \rho gh`

Putting the given values into the above formula as follows.

P =
`P_(atm) + \rho gh`

=
`98700 Pa + 13534 * 9.81 * 0.03 m`

= 102683.05 Pa

= 102.68 kPa

thus, we can conclude that the pressure of the given methane gas is 102.68 kPa.