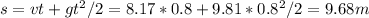Question

Calculate the height (in m) of a cliff if it takes 2.47 s for a rock to hit the ground when it is thrown straight up from the cliff with an initial velocity of 8.17 m/s. (Enter a number.)

Answer 1

9.68 m

Step-by-step explanation:

When a rock is thrown upward from the cliff, it travels upward until it stops midair, then it travel downward to the cliff throwing point, then down to the ground.

Let g = 9.81m/s2. We can calculate the time it takes for the rock to travel until it gets to maximum height, aka speed = 0 using the following equation of motion

`v = v_0 + gt`

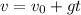
where v0 = 8.17 m/s is the initial upward speed, v = 0m/s is the speed at maximum height

0 = 8.17 - 9.81t

9.81t = 8.17

t = 8.17/9.81 = 0.833 s

According to law of energy conservation, rock would have the same kinetic energy when it fall back to it's throwing point. This means the speed when it travels back to it throwing point would be the same as the launch speed, 8.17m/s, but downward.

It would take the same amount of time t = 0.833s for the rock to gain back that much speed.

So the total time it takes for the rock to travel upward and back to its throwing point is t = 0.833 + 0.833 = 1.665 s

As the total time it takes to hit the ground is 2.47s, the rock would need an additional of 2.47 - 1.665 = 0.8s to travel from the throwing point downward to the ground at initial speed of 8.17m/s and a constant acceleration g = 9.81m/s2

The total distance covered, or height of the cliff would then be

`s = vt + gt^2/2 = 8.17*0.8 + 9.81*0.8^2/2 = 9.68 m`