Question

Let's say you are on the third story of an apartment building that has a swimming pool. For some insane reason you think it is a good idea to jump off your balcony into the swimming pool. If you are a height h above the ground and a distance r from the pool how far must you be running in terms of h and r to make into the pool and not end up as cement pizza? Are there any applications of this?

Answer 1

To make it into the pool you must run and jump at

`\displaystyle v_o=x.\sqrt{(g)/(2y)}`

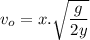
Step-by-step explanation:

Horizontal Launch

When an object is thrown with a specified initial speed in the horizontal direction, it describes a curved path that finishes when it hits the ground level after traveling certain horizontal distance x and a vertical height y from the launching point. The horizontal speed is always constant and the vertical speed increases due to the effect of gravity. It can be found that the horizontal distance reached by the object when launched at an initial speed in a given time t is

`x=v_o.t`

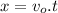
And the vertical distance is

`\displaystyle y=(g.t^2)/(2)`

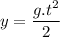
If t is the total flight time, then x and y are maximum and we can find a relation between them. Solving for t in the first equation

`\displaystyle t=(x)/(v_o)`

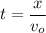
Substituting in the second equation

`\displaystyle y=(g)/(2)\left ( (x)/(v_o)\right )^2`

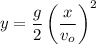
Rearranging

`\displaystyle \left ( (v_o)/(x)\right )^2=(g)/(2y)`

Solving for
`v_o`

`\displaystyle v_o=x.\sqrt{(g)/(2y)}`

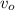
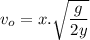
There are many applications for the horizontal launch. One common situation is when someone wants to drop something on certain terrain at a specific approximate point when traveling in a plane at a given height. Once the object is left fall, it has the same speed as the plane, so the plane speed can be estimated to make the best possible launch, or given that speed, we can know in advance where the object will reach ground level