Question

The number of bacteria, B left parenthesis h right parenthesis, in a certain population increases according to the following function, where time, h, is measured in hours:

B left parenthesis h right parenthesis equals 1425 e to the power of 0.15 h end exponent

How many hours will it take for the bacteria to reach 3700?

Round your answer to the nearest tenth, and do not round any intermediate computations.

Answer 1

About 6.4 hours.

Explanation:

We are given the function:

`\displaystyle B(h) = 1425e^(0.15h)`

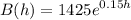
Which measures the population of bacteria B after h hours.

We want to determine the number of hours it will take for the population to reach 3700 bacteria.

Thus, substitute 3700 for B and solve for h:

`\displaystyle \begin{aligned} (3700) & = 1425e^(0.15h) \\ \\ e^(0.15h) & = (3700)/(1425) \end{aligned}`

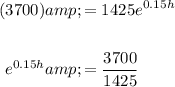
Take the natural log of both sides. This cancels the e on the left-hand side:

`\displaystyle \begin{aligned} \ln\left(e^(0.15h)\right) & = \ln(3700)/(1425) \\ \\ 0.15h & = \ln(3700)/(1425) \\ \\ h &= (\ln(3700)/(1425))/(0.15) \\ \\ & \approx 6.4\text{ hours} \end{aligned}`

In conclusion, it will take about 6.4 hours for the population of the bacteria to reach 3700.