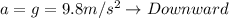Question

An egg is thrown nearly vertically upward from a point near the cornice of a tall building. It just misses the cornice on the way down and passes a point a distance 38.0m below its starting point at a time 5.00 s after it leaves the thrower's hand. Air resistance may be ignored.a. what is the inital speed of the egg?b. how high does it rise above the starting point?c. What is the magnitude of its velocity at the highest point?d. What is the magnitude of its acceleration at the highest point?

Answer 1

To solve this problem we will apply the linear motion kinematic equations. We will start by finding the initial velocity through the position equation as a function of velocity and acceleration with respect to time. Later we will find the maximum height through the energy conservation equations.

For the last two parts we will make a couple of conclusions that will give us the answer directly.

a) From the distance formula

`x(t)=v_0t+(1)/(2)at^2`

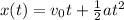
Here

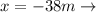`x=-38 m \rightarrow` From our reference point

`a=-g=9.8 m/s^2`

`-38m=v(5)+(1)/(2)(-9.8m/s^2)(5)^2`

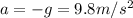
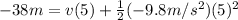
Solving for v,

`v=16.9m/s`

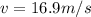
So the initial speed of the egg is 16.9 m/sec

B) At highest point K.E=P.E (conservation of energy)

`(1)/(2)mv^2=mgh`

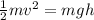
Rearranging to find the height we have,

`h=((v^2)/(2g))`

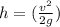
Replacing,

`h = (16.9^2 )/(2*9.8)`

`h =14.57 m`

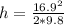
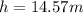
Height travelled by the egg is 14.57 m

C) When the body reaches its maximum point of height, the force of gravity begins to take effect, so the speed becomes 0 and its direction changes. Accordingly, the speed at its highest point is 0.

`v=0 m/s`

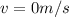
D) As we mentioned earlier at its highest point the acceleration is in the direction of the center of the earth, therefore the value of the acceleration will be the equivalent to that exerted by the gravitational force, like this:

`a=g=9.8 m/s^2 \rightarrow Downward`