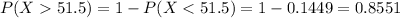Question

A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 50.05 and 60.06 minutes. Find the probability that a given class period runs greater thangreater than 51.5 minutes.

Answer 1

`P(X<51.5) = (51.5-50.05)/(10.01)=0.1449`

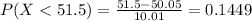
And then we can calculate the probability of interest using the complement rule:

`P(X>51.5) = 1-P(X<51.5) = 1-0.1449=0.8551`

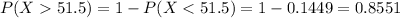
Explanation:

Let's assume that the random variable X ="Lengths of her classes", and we know that the distribution for X is given by:

`X \sim Unif (a=50.05, b= 60.06)`

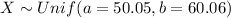
The expected value is given by:

`E(X) = (b+a)/(2)=(60.06+50.05)/(2)=55.055`

And the variance given by:

`Var(X) = ((b-a)^2)/(12)=((60.06-50.05)^2)/(12)=8.35`

The density function is given by:

`f(x) = (x)/(b-a)=(1)/(60.06-50.05)= 0.099  , 50.05 \leq X \leq 60.06`

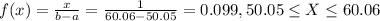
And 0 for other case.

And on this case we want to find the following probability
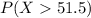`P(X>51.5)` first we need to calculate
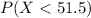`P(X<51.5)`, so we can calculate this with the following integral:

`P(X<51.5) = \int_(50.05)^(51.5) (1)/(10.01) dx = (1)/(10.01) x\Big|_(50.05)^(51.5)`

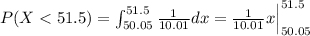
And after evaluate using the fundamental calculus theorem we got:

`P(X<51.5) = (51.5-50.05)/(10.01)=0.1449`

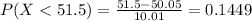
And then we can calculate the probability of interest using the complement rule:

`P(X>51.5) = 1-P(X<51.5) = 1-0.1449=0.8551`