Answer:
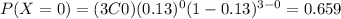
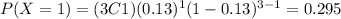
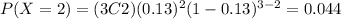
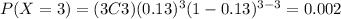
And then our probability distribution would be given by:
X 0 1 2 3
P(X) 0.659 0.295 0.044 0.002
Explanation:
Previous concepts
A Bernoulli trial is "a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted". And this experiment is a particular case of the binomial experiment.
The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".
The probability mass function for the Binomial distribution is given as:
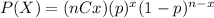
Where (nCx) means combinatory and it's given by this formula:
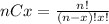
Solution to the problem
For this case we know that 13% is the percent of parents that allow children under age of 13 to stay home alone after school. So then that represent our parameter p. Now we know that they select 3 people so then n =3.
Our random variable X ="number of these parents who allow their children under age of 13 to stay home alone after school" follows a binomial distribution:
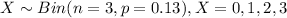
And we can find the probability for each possible value of X like this:
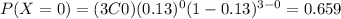
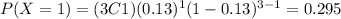
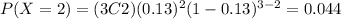
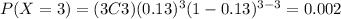
And then our probability distribution would be given by:
X 0 1 2 3
P(X) 0.659 0.295 0.044 0.002