Question

A spacecraft at rest has moment of inertia of 100 kg-m^2 about an axis of interest. If a 1 newton thruster with a 1 meter moment arm is fired orthogonal to the axis of interest for 1 minute, how far has the vehicle rotated when the firing is complete?Also, what details of a real system does this question neglect?

Answer 1

To solve this problem we will apply the concepts related to translational torque, angular torque and the kinematic equations of angular movement with which we will find the angular displacement of the system.

Translational torque can be defined as,

`\tau = Fd`

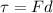
Here,

F = Force

d = Distance which the force is applied

`\tau = (1N)(1m)`

`\tau = 1N\cdot m`

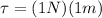
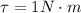
At the same time the angular torque is defined as the product between the moment of inertia and the angular acceleration, so using the previous value of the found torque, and with the moment of inertia given by the statement, we would have that the angular acceleration is

`\tau = I\alpha`

`\alpha = (\tau)/(I)`

`\alpha = (1N\cdot m)/(100kg\cdot m^2)`

`\alpha = 0.01rad/s^2`

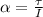
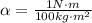
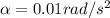
Now the angular displacement is

`\theta = \omega_0 t + (1)/(2)\alpha t^2`

Here

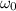`\omega_0`= Initial angular velocity

t = time

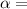`\alpha =`Angular acceleration

`\theta`= Angular displacement

Time is given as 1 minute, in seconds will be

`t = 1m = 60s`

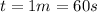
There is not initial angular velocity, then

`\theta= (1)/(2)\alpha t^2`

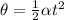
Replacing,

`\theta= (1)/(2)(0.01)(60)^2`

`\theta = 18rad`

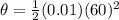
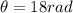
The question neglects the effect of gravitational force.