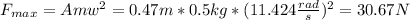Answer:
a)
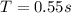
b)
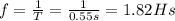
c)

d)
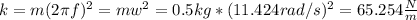
e)
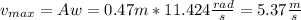
f)
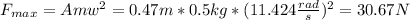
Step-by-step explanation:
Part a
For this case we know that the mass repeat its motion every 0.550 s. And that's the definition of period so for this case
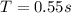
Part b
By definition the frecuency is the inverse of the period so we have this:
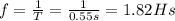
Part c
The angular fecuency is defined with the following formula:
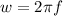
And since we have the frequency we can replace:

Part d
For this case we know that the period is given by:
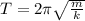
And if we solve for k we have this:


And since
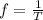 we can rewrite this expression like this:
we can rewrite this expression like this:
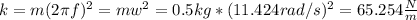
Part e
The maximum speed for an oscillator is given by this formula:
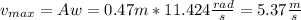
Part f
The maximum force is given by this formula:

And the
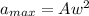 because the acceleration is the derivate of the velocity, so then we have:
because the acceleration is the derivate of the velocity, so then we have: