Question

A tower is 200 feet tall. To the nearest degree, find the angle of elevatio n from a point 50 feet from the base of the tower to the top of tower.

Answer 1

Answer:
`75.96^(\circ)`.

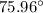Explanation:

By considering the given information we draw a picture to represent the situation ( given in attachment)

Since the tower stands vertical to the ground , therefore , the triangle is a right triangle.

Let x be the angle of elevation from a point 50 feet from the base of the tower to the top of tower.

According to the trigonometry , the tangent of an angle is the ratio of "the side opposite to angle" to "the side adjacent to the angle".

For the triangle below ,
`\tan x=(200)/(50)=4\\\\ x=\tan^(-1)(4)=1.32581766\ radians\ [\text{By scientific calculator}]\\\\=1.32581766*(180^(\circ))/(\pi)\ \\\\=75.9637563^(\circ)=75.96^(\circ)`

[Note:To convert radians into degrees we multiply it by
`180^(\circ)}` and divide it by
`\pi`]

Hence, the angle of elevation from a point 50 feet from the base of the tower to the top of tower is
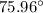`75.96^(\circ)`.