Question

Hey I was just wondering if anyone can give me a better explanation on how to work with Negative numbers and and fractions when factorisation. It’s just a bit confusing on how to work those kind of equations out. I’ll put a picture of like examples of the questions I have to answer, all I’m asking is just a basic explanation and a step by step equation on how it works

Thanks

Answer 1

see explanation

Explanation:

Given

`(6(2a-4c)-6(6a-4b)+3(4b-8c))/(4)`

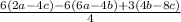
Distribute the 3 parenthesis on the numerator

=
`(12a-24c-36a+24b+12b-24c)/(4)`

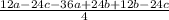
Collect like terms on the numerator

=
`(-24a+36b-48c)/(4)`

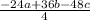
Divide each of the terms on the numerator by 4

=
`(-24a)/(4)` +
`(36b)/(4)` +
`(-48c)/(4)`

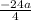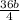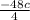
= - 6a + 9b - 12c ← factor out - 3 from each term

= - 3(2a - 3b + 4c)

Compare with

X(2a + Bb + Cc) to obtain

X = - 3, B = - 3, C = 4