Question

Various problems with data collection can cause some observations to be missing. Suppose a data set has 20 cases. Here are the values of the variable x for 10 of these cases: 17, 6, 12, 14, 20, 23, 9, 12, 16, 21 The values for the other ten cases are missing. One way to deal with missing data is called imputation. The basic idea is that missing values are replaced, or imputed, with values that are based on an analysis of the data that are not missing. For a data set with a single variable, the usual choice of a value for imputation is the mean of the values that are not missing. (a) Compute the mean and standard deviation for the 10 cases for which x is not missing. (b) Create a new data set with 20 cases by using imputation where you set the values for the 10 missing cases equal to the mean that you computed in the previous part. Compute the mean and standard deviation for this new data set with 20 cases. (c) Summarize what you have learned about the possible effects of this type of imputation on the mean and the standard deviation.

Answer 1

a) Mean= 15, standard deviation= 5.1575

b) Mean= 15, standard deviation= 3.6469

c) See below

Explanation:

(a) Compute the mean and standard deviation for the 10 cases for which x is not missing.

The mean using the ten known values is

`\bar x=(17+6+12+14+20+23+9+12+16+21)/(10)=15`

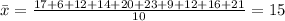
The standard deviation is

`\small s=\sqrt{((17-15)^2+(6-15)^2+(12-15)^2+(14-15)^2+(20-15)^2+(23-15)^2+(9-15)^2+(12-15)^2+(16-15)^2+(21-15)^2)/(10)}=5.1575`

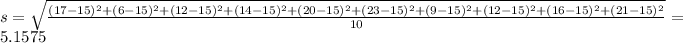
(b) Create a new data set with 20 cases by using imputation where you set the values for the 10 missing cases equal to the mean that you computed in the previous part. Compute the mean and standard deviation for this new data set with 20 cases.

The new data set would be

17, 6, 12, 14, 20, 23, 9, 12, 16, 21, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15

The new mean for this set of values would be then

`\bar x=(\displaystyle\sum_(i=1)^(20)x_i)/(20)=15`

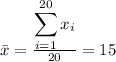
The new standard deviation is now

`s=\sqrt{(\displaystyle\sum_(i=1)^(20)(x_i-\bar x)^2)/(20)}=3.6469`

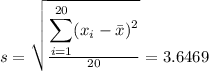
(c) Summarize what you have learned about the possible effects of this type of imputation on the mean and the standard deviation.

Obviously, this way of imputation is somewhat arbitrary and will produce a set of data undoubtedly skewed.

It could possibly be a sensible way of imputing data if the amount of missing data is very little compared to the whole set, for example one or two data in a set of 100, but in this case we have 50% of missing data and it makes no sense this procedure.