Question

Suppose that you had the following data set. 100 200 250 275 300 Suppose that the value 250 was a typo, and it was suppose to be 260. How would the value of the standard deviation change? Group of answer choices It would decrease significantly. It would increase significantly. It would pretty much stay the same. Can not be determined.

Answer 1

`\bar X_(B) =(\sum_(i=1)^5 X_i)/(n) = (1125)/(5)=225`

`s_B=\sqrt{(\sum_(i=1)^5 (X_i- \bar X)^2)/(n-1)}=79.057`

`\bar X_(N) =(\sum_(i=1)^5 X_i)/(n) = (1135)/(5)=227`

`s_N=\sqrt{(\sum_(i=1)^5 (X_i- \bar X)^2)/(n-1)}=79.968`

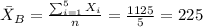
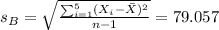
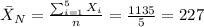
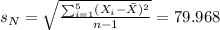
If we see after changing the value of 250 by 260 we don't have a significant difference between the two deviations calculated.

The difference is just
`dif= 79.968-79.057=0.911`

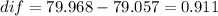
So then the best conclusion for this case is:

It would pretty much stay the same.

Explanation:

Notation

B = mean the before case (with 250), N = mean the new case (with 260 instead of 250)

Before Case

Data: 100 200 250 275 300

We can calculate the sample mean and we got:

`\bar X_(B) =(\sum_(i=1)^5 X_i)/(n) = (1125)/(5)=225`

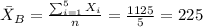
And the sample standard deviation with:

`s_B=\sqrt{(\sum_(i=1)^5 (X_i- \bar X)^2)/(n-1)}=79.057`

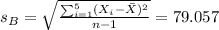
New case

Data: 100 200 260 275 300

We can calculate the sample mean and we got:

`\bar X_(N) =(\sum_(i=1)^5 X_i)/(n) = (1135)/(5)=227`

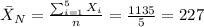
And the sample standard deviation with:

`s_N=\sqrt{(\sum_(i=1)^5 (X_i- \bar X)^2)/(n-1)}=79.968`

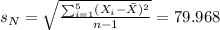
If we see after changing the value of 250 by 260 we don't have a significant difference between the two deviations calculated.

The difference is just
`dif= 79.968-79.057=0.911`

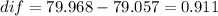
So then the best conclusion for this case is:

It would pretty much stay the same.