Question

Write an expression for the 12th partial sum of the series 3/2+7/3+19/6+... using summation notation

Answer 1

The 12th partial sum of the series
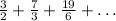`\( (3)/(2) + (7)/(3) + (19)/(6) + \ldots \)` can be expressed as
`\( \sum_(n=1)^(12) (2n-1)/(2(n-1)) \)`.

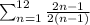Step-by-step explanation:

The 12th partial sum of the series
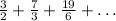`\( (3)/(2) + (7)/(3) + (19)/(6) + \ldots \)` can be expressed using summation notation as:

`\[ S_(12) = \sum_(n=1)^(12) (2n-1)/(2(n-1)) \]`

Step-by-step explanation:

1. The series starts from n = 1 and goes up to n = 12, as indicated by the subscript 12 in
   `\( S_(12) \)`.
2. 
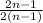   `\( (2n-1)/(2(n-1)) \)` represents the general term of the series. For each term with index n, the numerator is
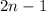   `\( 2n-1 \)` and the denominator is
   `\( 2(n-1) \)`.
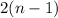3. The sigma notation
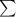   `\( \sum \)` is used to denote the summation. In this case, it adds up the terms for each n from 1 to 12.

In conclusion,
`\( S_(12) \)` represents the sum of the first 12 terms of the given series using the specified formula.

Answer 2

Did you ever find the actual answer?

Step-by-step explanation: