Question

If ch4 and c4h8 are released simultaneously at ends of a 50.0cm long glass tube, at what distance from the left end of the tube will they meet

Answer 1

They meet at the distance of 32.5 cm

Step-by-step explanation:

The rate of diffusion is inversely proportional to the molar mass of gases.

If diffusion is represented as d and mass of gases as M. Then , rate is given as:

`d=k\sqrt{(1)/(M)}`

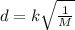
For , two gases

`(d_(1))/(d_(2))=\sqrt{(M_(2))/(M_(1))}`

First , Calculate the ,molar mass of each gas :

CH4 = 1 (mass of C) + 4(mass of H)

= 1(12)+4(1)

= 12 + 4 = 16 gram

M1 = 16 gram

C4H8 = 4(mass of C) + 8(Mass of H)

= 4(12) + 8(1)

= 48 + 8

M2 = 56 grams

d1 is diffusion of CH4

d2 = diffusion of C4H8

`(d_(1))/(d_(2))=\sqrt{(M_(2))/(M_(1))}`

`(d_(1))/(d_(2))=\sqrt{(56)/(16)`}

`(d_(1))/(d_(2)) = 1.87`

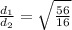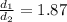
This means CH4 diffuse 1.87 times faster than C4H8

Now, the mathematical part

If velocity of C4H8 = 1 cm/sec , then velocity of CH4 = 1.87 cm/sec

v1 = 1.87 cm/sec

v2 = 1 cm/sec

Let both meet at time "t". If distance travelled by CH4(s1) = x , then remaining(s2) distance (50-x) is travelled by C4H8

(see the attached image)

`time =(distance)/(speed)`

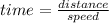
since both meet at same time so t = constant.

`(s1)/(v1)=(s2)/(v2)`

`(x)/(1.87)(50-x)/(1.00)`

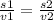
on solving for x we get,

x = 17.42 cm

from the other side the distance is (50 - x)

= 50 - 17.42 = 32.5 cm