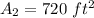Answer:
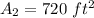
Explanation:
Let w and l be the width and length of the garage.
Let
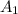 and
and
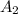 be the area of garage at present and new garage.
be the area of garage at present and new garage.
Given:
The area of the garage at present
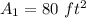
And he planed to tripling the dimensions of the garage.
We need to find the area of the new garage.
Solution:
We know the area of the rectangular garage.
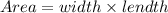
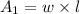
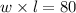 ---------------(1)
---------------(1)
The dimension of the new garage is triple, so the area of the new garage is.
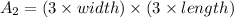

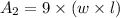
Substitute
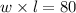 from equation 1.
from equation 1.
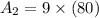
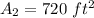
Therefore, the area of the new garage