Question

Verify that these two are inverses using composition of functions and show your work

Answer 1

f(g(x)) = g(f(x)) = x

Explanation:

To prove two functions, say f(x) and g(x) are inverses to each other, we take the composition of the two functions: f(g(x)) and g(f(x)) and prove that:

f(g(x)) = g(f(x)) = x, x is the identity function

Now, given:

`$ f(x) = \frac{\sqrt[3]{x + 4}}{7} $` and
`$ g(x) = (7x)^3 - 4 $`

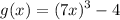
Calculate: f(g(x)):

`$ f(g(x)) = f((7x)^3 - 4) $`

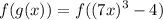
It means to substitute
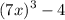`$ (7x)^3 - 4$` in place of x.

Therefore, we get:

`$ f(g(x)) = \bigg \{ \frac{ \sqrt[3]{(7x)^3 - 4 + 4}}{7} \bigg \} $`

`$ f(g(x)) = \bigg \{ \frac{ \sqrt[3]{(7x)^3}}{7} \bigg \} $`

`$ = ((7x))/(7) $`

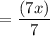
= x, the identity function.

Now compute g(f(x))

`$ g(x) = (7x)^3 - 4 $$ \therefore g(x) = 343x^3 - 4 $`

Now,
`$ g(f(x)) = 343 \bigg \{ \bigg ( \frac{\sqrt[3]{x + 4}}{7} \bigg ) ^3 \bigg \} - 4`

`$ = 7^3 (x + 4)/(7^3) - 4 $`

`$ = (x + 4) - 4 $`

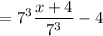
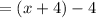
= x

We have proved f(g(x)) = g(f(x)) = x. Hence, they are inverses of each other.