Question

A quadratic equation is given below.

2x² - 8x + c = y
If the graph of this quadratic equation has a minimum value at (2, 10), what is the value of c?
18
-6
-2
14

Answer 1

c = 18

Explanation:

The minimum value of the quadratic falls on the graph of the quadratic (parabola). So we can substitute the x and y values from the coordinate pair and use algebra to solve for c.

Given

x = 2

y = 10

Putting in the equation, we have:

`2(2)^2 -8(2)+c=10`

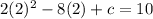
Solving for c:

`2(2)^2 -8(2)+c=10\\8-16+c=10\\-8+c=10\\c=10+8\\c=18`

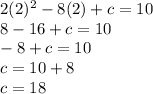
So,

The value of c is 18