Question

How do I solve the quadratic equation by factoring? 3x^2+12x+12=0

Answer 1

x = -2

Explanation:

`3x^2+12x+12=0`

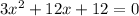
First, try to factor out a common factor from every term.

The coefficients are 3, 12, and 12.

The GCF (greatest common factor) of 3, 12, and 12 is 3, so factor out a 3 from all terms.

`3(x^2+4x+4)=0`

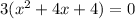
Now divide both sides by 3.

`x^2+4x+4=0`

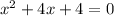
You have a quadratic trinomial of the form x^2 + ax + b.

To factor it, you need to find two numbers that multiply to b and add to a. Call these two numbers p and q.

Then the factorization is (x + p)(x + q).

In your case, you have

`x^2 + 4x + 4 = 0`

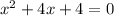
In this case, a = 4 and b = 4.

You need two numbers that multiply to 4 and add to 4.

The numbers are 2 and 2.

Then the factorization is

`(x + 2)(x + 2) = 0`

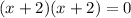
Now set each factor equal to zero and solve for x.

x + 2 = 0 or x + 2 = 0

x = -2 or x = -2

Answer: x = -2