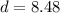Question

Find the difference between each pair of points
(3,-4) and (-3,2)

Answer 1

`d=6√(2)`

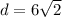
or

`d = 8.48`

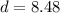
Explanation:

Given:

The given points are (3,-4) and (-3,2).

Assume, we need to find the distance between two points.

Solution:

Distance formula of the two points.

`d = \sqrt{(x_(1)-x_(2))^(2)+(y_(1)-y_(2))^(2) }`

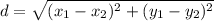
Now we substitute give points (3,-4) and (-3,2) in above equitation.

`d=\sqrt{(-3-3)^(2)+(2-(-4))^(2)}`

`d=\sqrt{(-6)^(2)+(2+4)^(2)}`

`d=\sqrt{36+(6)^(2)}`

`d=√(36+36)`

`d=√(72)`

`d=6√(2)`

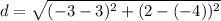
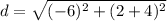
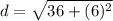
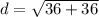
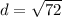
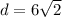
or

`d = 8.48`

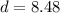
Therefor, the distance between the given points
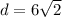`d=6√(2)` or
`d = 8.48`