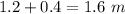Question

In a basketball game, a ball leaves a player's hand 6.1 m downrange from the basket from a height of 1.2 m below the level of the basket. If the initial velocity of the ball is 7.8m [55 degrees above the horizontal] in line with the basket, will the player score a basket? If not, by how much will the ball miss the basket?

Answer 1

The ball missed the basket by 1.6 meters

Step-by-step explanation:

Projectile Motion

It's when an object is moving in a two-dimensional space, being thrown with an initial speed and angle respect to the horizontal direction. The horizontal distance traveled by the object is given by

`x=vo.cos\theta .t`

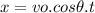
And the vertical height above the level of the launch is

`\displaystyle y=vo.sin\theta. t-(gt^2)/(2)`

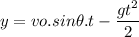
The basketball player throws the ball with initial speed
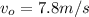`v_o=7.8 m/s` at an angle of
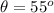`\theta=55^o`. The horizontal distance to the basket (as suggested by the 'downrange' word) is x=6.1 m. We need to find out if the ball reaches the basket at a height y=1.2 m above the launching point.

From the equation

`x=vo.cos\theta .t`

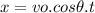
We'll solve for t and find the flight time until the horizontal distance is reached by the ball

`\displaystyle t=(x)/(vo.cos\theta)`

`\displaystyle t=(6.1)/((7.8).cos55^o)=1.363\ sec`

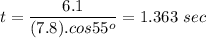
Now, we use this time to find y

`\displaystyle y=(7.8).sin55^o . (1.363)-((9.8)(1.363)^2)/(2)`

`y=-0.4\ m`

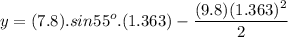
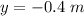
The negative sign indicates the ball fell below the launching point, and missed the basket by

`1.2+0.4 = 1.6\ m`