Question

Which equation describes the graph?

a:y=-|x+2|
b:y=-|x|+2
c:y=-|x-2|
d:y=-|x|-2

Answer 1

OPTION C: y = - |x - 2|

Explanation:

To solve problems of this type take any two points on the graph. We take two points:

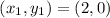`$ (x_1, y_1) = (2, 0) $` This means that when x = 2, y = 0.

And
`$ (x_2, y_2) = (0, -2) $`

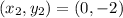
These two points are on the given line.

So, these two points are substituted to check if they satisfy the given equation.

OPTION A: y = - |x + 2|

Substituting (2, 0):

LHS = y = 0

RHS = - |2 + 2| = - 4 ≠ 0

So, this option is eliminated.

OPTION B: y = - |x| + 2

Substitute (x, y) = (2, 0)

LHS = 0

RHS = - |2| + 2 = - 2 + 2 = 0

LHS = RHS

Now, check for (0, -2)

LHS = -2

RHS = - |0| + 2|

= - |0| + 2 = 2 ≠ -2

So, this option is eliminated as well.

OPTION C: y = - |x - 2|

Substitute (2, 0)

LHS = 0

RHS = - |2 - 2| = 0

LHS = RHS

Now, substitute (0, -2)

LHS = -2

RHS = - |0 - 2|

= - |- 2|

= - 2

∴ LHS = RHS for both the points.

OPTION D: y = - |x| - 2

Substitute (2, 0)

LHS = 0

RHS = - |2| - 2

= - 2 - 2

= - 4

This option is eliminated as well.

So, OPTION C is our answer since it satisfies the points.

NOTE: Points satisfying the equation of the graph is only a necessary condition not a sufficient one.