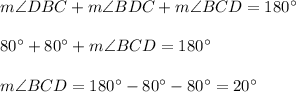Question

In the diagram, AD=CD=CB and measure of angle A=40°. How many degrees are in angle DCB?​

Answer 1

`20^(\circ)`

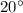
Explanation:

Consider triangle ACD. This triangle is isosceles triangle, because AD = DC. Angles adjacent to the base AC are congruent abgles, so

`m\angle DAC=m\angle DCA=40^(\circ)`

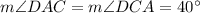
The sum of the measures of all interiror angles in the triangle is always
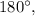`180^(\circ),` then

`m\angle DAC+m\angle DCA+m\angle ADC=180^(\circ)\\ \\40^(\circ)+40^(\circ)+m\angle ADC=180^(\circ)\\ \\m\angle ADC=180^(\circ)-40^(\circ)-40^(\circ)=100^(\circ)`

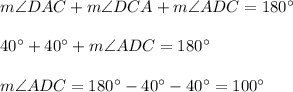
Angles ADC and BDC are supplementary angles (add up to
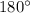`180^(\circ)`), then

`m\angle BDC=180^(\circ)-100^(\circ)=80^(\circ)`

Consider triangle BCD. This triangle is isosceles triangle because BC = DC. Angles adjacent to the base BD are congruent abgles, so

`m\angle BDC=m\angle DBC=80^(\circ)`

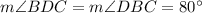
The sum of the measures of all interiror angles in the triangle is always
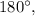`180^(\circ),` then

`m\angle DBC+m\angle BDC+m\angle BCD=180^(\circ)\\ \\80^(\circ)+80^(\circ)+m\angle BCD=180^(\circ)\\ \\m\angle BCD=180^(\circ)-80^(\circ)-80^(\circ)=20^(\circ)`