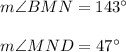Answer:
Therefore,
A. ∠BMN + ∠MND = 180°
B . x = 35
C.
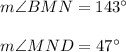
Explanation:
Given:
Consider the Figure below such that
AB || CD
PQ as transversal
m∠BMN = (4x+3) and
m∠MND = (x+2)
To Find:
1. Relation between interior angles
2. x = ?
3. m∠BMN = ? and m∠MND = ?
Solution:
Same Side Interior Postulate:
The same-side interior angle theorem states that "when two lines that are parallel are intersected by a transversal line, the same-side interior angles that are formed are supplementary, or add up to 180 degrees".
As, AB || CD
PQ as transversal
∠BMN and ∠MND are Same Side Interior angles.
∴ ∠BMN + ∠MND = 180° ......Relationship between the angles.
Substituting the values we get
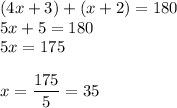
Substitute 'x' in ∠BMN and ∠MND we get
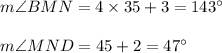
Therefore,
A. ∠BMN + ∠MND = 180°
B . x = 35
C.