Answer:
See explanation and attachment
Explanation:
a) To graph
 , we need to plot some few points.
, we need to plot some few points.
When x=-2,
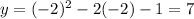 so we plot (-2,7).
so we plot (-2,7).
When x=-1,
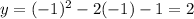 so we plot (-1,2)
so we plot (-1,2)
When x=0,
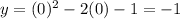 so we plot (0,-1)
so we plot (0,-1)
When x=1,
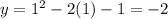 so we plot (1,-2)
so we plot (1,-2)
When x=2,
 so we plot (2,-1)
so we plot (2,-1)
We then draw a smooth curve through the points to obtain the curve in the attachment.
b) The graph intersected the x-axis (y=0) at x=-0.41 and x=2.41. These are the roots.
c) For the line y=2x-3
When x=0, y=2(0)-3=-3 so we plot (0,-3)
When x=1, y=2(1)-3=-1 So we plot (1,-1)
We draw a straight line through these two points to intersect the parabola as shown on the graph.
d) To solve

and
 simultaneously using the graph, we look for the point of intersection of the parabola and the straight line.
simultaneously using the graph, we look for the point of intersection of the parabola and the straight line.
The solution is (0.59,-1.83) and (3.41,3.83)