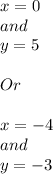Question

Solve algebraically the simultaneous equations

X^2 + Y^2 =25
Y-2X = 5

Answer 1

Therefore the solutions are

`x=0\\and\\ y =5\\\\Or\\\\x=-4\\and\\y=-3`

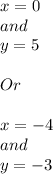
Explanation:

Given:

`x^(2) + y^(2) =25` .........( 1 )

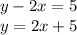`y-2x = 5\\y=2x+5` ................( 2 )

To Find:

x = ?

y = ?

Solution:

Substituting ' y ' in Equation 1 we get

`x^(2)+(2x+5)^(2) =25`

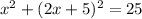
Using identity (A+B)²=A²+2AB+B² we get

`x^(2)+4x^(2)+20x+25=25\\\\5x^(2)+20x=0\\5x(x+4)=0\\5x=0\ or\ x+4=0\\x=0\ or\ x= -4`

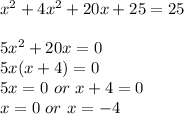
Now Substitute x =0 in equation 2 we get

`y=2* 0+5=5`

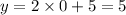
Or

Now Substitute x =-4 in equation 2 we get

`y=2* -4+5=-3`

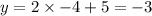
Therefore the solutions are

`x=0\\and\\ y =5\\\\Or\\\\x=-4\\and\\y=-3`