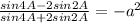Question

If tanA=a
then find sin4A-2sin2A/ sin4A+2sin2A​

Answer 1

The value of the given expression is

`(sin4A-2sin2A)/(sin4A+2sin2A)=-a^2`

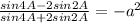
Step by step Explanation:

Given that
`tanA=a`

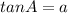
To find the value of
`(sin4A-2sin2A)/(sin4A+2sin2A)`

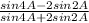
Let us find the value of the expression :

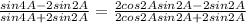`(sin4A-2sin2A)/(sin4A+2sin2A)=(2cos2Asin2A-2sin2A)/(2cos2Asin2A+2sin2A)` ( by using the formula
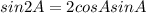`sin2A=2cosAsinA` here A=2A)

`=(2sin2A(cos2A-1))/(2sin2A(cos2A+1))`

`=((cos2A-1))/((cos2A+1))`

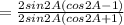
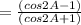
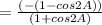`=((-(1-cos2A)))/((1+cos2A))`(using
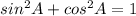`sin^2A+cos^2A=1` here A=2A)

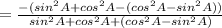`=(-(sin^2A+cos^2A-(cos^2A-sin^2A)))/(sin^2A+cos^2A+(cos^2A-sin^2A))`(using
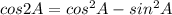`cos2A=cos^2A-sin^2A` here A=2A)

`=(-(sin^2A+cos^2A-cos^2A+sin^2A))/(sin^2A+cos^2A+(cos^2A-sin^2A))`

`=(-(sin^2A+sin^2A))/(cos^2A+cos^2A)`

`=(-2sin^2A)/(2cos^2A)`

`=-(sin^2A)/(cos^2A)`

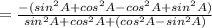
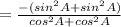
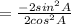
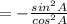
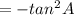`=-tan^2A` ( using
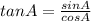`tanA=(sinA)/(cosA)` here A=2A )

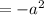`=-a^2` (since tanA=a given )

Therefore
`(sin4A-2sin2A)/(sin4A+2sin2A)=-a^2`